Supernova light curves#
In this example we will explore a physical example of fitting a supernova light curve model to data
Nested Sampling with JAX-bandflux#
This notebook demonstrates how to run the nested sampling procedure for supernovae SALT model fitting using the JAX-bandflux package (as implemented in ns.py). We will install the package, load the data, set up and run the nested sampling algorithm, and finally produce a corner plot of the posterior samples.
For more examples and the complete codebase, visit the JAX-bandflux GitHub repository. The academic paper associated with this work can be found here.
# Install JAX-bandflux and its dependencies
!pip install jax-bandflux
# Install BlackjaxNS and distrax
!pip install git+https://github.com/handley-lab/blackjax@proposal
!pip install git+https://github.com/google-deepmind/distrax
# Additional dependencies
!pip install jax jaxlib anesthetic matplotlib tqdm
Importing Libraries and Loading Data#
In this section, we import the required libraries and load the supernova light curve data using the function load_and_process_data. This function will also register the required bandpasses, process the data, and prepare it for modelling.
import jax
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
import tqdm
from blackjax.ns.utils import log_weights
from jax_supernovae.salt3 import optimized_salt3_multiband_flux
from jax_supernovae.data import load_and_process_data
from jax_supernovae.bandpasses import register_bandpass, get_bandpass, register_all_bandpasses
from jax_supernovae.utils import save_chains_dead_birth
from anesthetic import read_chains, make_2d_axes
import os
# Set flag to use fixed redshift
fix_z = True
# Load and process the data (ensure your data files are in the 'data' directory)
times, fluxes, fluxerrs, zps, band_indices, bridges, fixed_z = load_and_process_data('19dwz', data_dir='data', fix_z=fix_z)
print('Data loaded:')
print('Observation times shape:', times.shape)
print('Flux measurements shape:', fluxes.shape)
Loading data from /Users/yallup/projects/nested-sampling-book/env/lib/python3.12/site-packages/jax_supernovae/data/19dwz/all.phot
Data loaded:
Observation times shape: (33,)
Flux measurements shape: (33,)
Setting Up the Nested Sampling Algorithm#
Here we define the necessary functions for nested sampling. These include the log prior and log likelihood functions, which will be utilised by the sampling algorithm from Blackjax. The parameters being fitted are t0, x0 (expressed in log scale), x1, c and optionally log_sigma. Prior bounds and distributions are defined accordingly.
Nested sampling settings#
On a GPU, you might consider setting ‘n_delete’ to a value close to n_live/2, e.g.,
NS_SETTINGS['n_delete'] = NS_SETTINGS['n_live'] // 2. This change can substantially speedup the nested sampling algorithm.
# Nested sampling settings
NS_SETTINGS = {
'n_delete': 20,
'n_live': 200,
'num_mcmc_steps_multiplier': 5
}
Setup prior bounds and distributions#
In this section, we define the prior bounds and distributions for our SALT3 model parameters. The priors are uniform distributions over physically meaningful ranges for each parameter. For fixed redshift cases, we fit for t0 (time of peak brightness), x0 (overall amplitude), x1 (light curve stretch), and c (colour). When redshift is not fixed, we also fit for z (redshift).
import os
import distrax
import blackjax
# Define prior bounds for parameters
PRIOR_BOUNDS = {
't0': {'min': 58000.0, 'max': 59000.0},
'x0': {'min': -5.0, 'max': -2.6},
'x1': {'min': -4.0, 'max': 4.0},
'c': {'min': -0.3, 'max': 0.3},
'log_sigma': {'min': -3.0, 'max': 1.0}
}
# Set whether to fit sigma (extra free parameter)
fit_sigma = False
if fix_z:
param_bounds = {
't0': (PRIOR_BOUNDS['t0']['min'], PRIOR_BOUNDS['t0']['max']),
'x0': (PRIOR_BOUNDS['x0']['min'], PRIOR_BOUNDS['x0']['max']),
'x1': (PRIOR_BOUNDS['x1']['min'], PRIOR_BOUNDS['x1']['max']),
'c': (PRIOR_BOUNDS['c']['min'], PRIOR_BOUNDS['c']['max'])
}
if fit_sigma:
param_bounds['log_sigma'] = (PRIOR_BOUNDS['log_sigma']['min'], PRIOR_BOUNDS['log_sigma']['max'])
prior_dists = {
't0': distrax.Uniform(low=param_bounds['t0'][0], high=param_bounds['t0'][1]),
'x0': distrax.Uniform(low=param_bounds['x0'][0], high=param_bounds['x0'][1]),
'x1': distrax.Uniform(low=param_bounds['x1'][0], high=param_bounds['x1'][1]),
'c': distrax.Uniform(low=param_bounds['c'][0], high=param_bounds['c'][1])
}
if fit_sigma:
prior_dists['log_sigma'] = distrax.Uniform(low=param_bounds['log_sigma'][0], high=param_bounds['log_sigma'][1])
else:
param_bounds = {
'z': (0.001, 0.2),
't0': (PRIOR_BOUNDS['t0']['min'], PRIOR_BOUNDS['t0']['max']),
'x0': (PRIOR_BOUNDS['x0']['min'], PRIOR_BOUNDS['x0']['max']),
'x1': (PRIOR_BOUNDS['x1']['min'], PRIOR_BOUNDS['x1']['max']),
'c': (PRIOR_BOUNDS['c']['min'], PRIOR_BOUNDS['c']['max'])
}
if fit_sigma:
param_bounds['log_sigma'] = (PRIOR_BOUNDS['log_sigma']['min'], PRIOR_BOUNDS['log_sigma']['max'])
prior_dists = {
'z': distrax.Uniform(low=param_bounds['z'][0], high=param_bounds['z'][1]),
't0': distrax.Uniform(low=param_bounds['t0'][0], high=param_bounds['t0'][1]),
'x0': distrax.Uniform(low=param_bounds['x0'][0], high=param_bounds['x0'][1]),
'x1': distrax.Uniform(low=param_bounds['x1'][0], high=param_bounds['x1'][1]),
'c': distrax.Uniform(low=param_bounds['c'][0], high=param_bounds['c'][1])
}
if fit_sigma:
prior_dists['log_sigma'] = distrax.Uniform(low=param_bounds['log_sigma'][0], high=param_bounds['log_sigma'][1])
@jax.jit
def logprior(params):
if fix_z:
if fit_sigma:
logp = (prior_dists['t0'].log_prob(params[0]) +
prior_dists['x0'].log_prob(params[1]) +
prior_dists['x1'].log_prob(params[2]) +
prior_dists['c'].log_prob(params[3]) +
prior_dists['log_sigma'].log_prob(params[4]))
else:
logp = (prior_dists['t0'].log_prob(params[0]) +
prior_dists['x0'].log_prob(params[1]) +
prior_dists['x1'].log_prob(params[2]) +
prior_dists['c'].log_prob(params[3]))
else:
if fit_sigma:
logp = (prior_dists['z'].log_prob(params[0]) +
prior_dists['t0'].log_prob(params[1]) +
prior_dists['x0'].log_prob(params[2]) +
prior_dists['x1'].log_prob(params[3]) +
prior_dists['c'].log_prob(params[4]) +
prior_dists['log_sigma'].log_prob(params[5]))
else:
logp = (prior_dists['z'].log_prob(params[0]) +
prior_dists['t0'].log_prob(params[1]) +
prior_dists['x0'].log_prob(params[2]) +
prior_dists['x1'].log_prob(params[3]) +
prior_dists['c'].log_prob(params[4]))
return logp
# Define the log likelihood functions
@jax.jit
def compute_single_loglikelihood(params):
if fix_z:
if fit_sigma:
t0, log_x0, x1, c, log_sigma = params
sigma = 10 ** log_sigma
else:
t0, log_x0, x1, c = params
sigma = 1.0
z = fixed_z[0]
else:
if fit_sigma:
z, t0, log_x0, x1, c, log_sigma = params
sigma = 10 ** log_sigma
else:
z, t0, log_x0, x1, c = params
sigma = 1.0
x0 = 10 ** log_x0
param_dict = {'z': z, 't0': t0, 'x0': x0, 'x1': x1, 'c': c}
model_fluxes = optimized_salt3_multiband_flux(times, bridges, param_dict, zps=zps, zpsys='ab')
model_fluxes = model_fluxes[jnp.arange(len(times)), band_indices]
eff_fluxerrs = sigma * fluxerrs
chi2 = jnp.sum(((fluxes - model_fluxes) / eff_fluxerrs) ** 2)
log_likelihood = -0.5 * (chi2 + jnp.sum(jnp.log(2 * jnp.pi * eff_fluxerrs ** 2)))
return log_likelihood
def sample_from_priors(rng_key, n_samples):
if fix_z:
if fit_sigma:
keys = jax.random.split(rng_key, 5)
return jnp.column_stack([
prior_dists['t0'].sample(seed=keys[0], sample_shape=(n_samples,)),
prior_dists['x0'].sample(seed=keys[1], sample_shape=(n_samples,)),
prior_dists['x1'].sample(seed=keys[2], sample_shape=(n_samples,)),
prior_dists['c'].sample(seed=keys[3], sample_shape=(n_samples,)),
prior_dists['log_sigma'].sample(seed=keys[4], sample_shape=(n_samples,))
])
else:
keys = jax.random.split(rng_key, 4)
return jnp.column_stack([
prior_dists['t0'].sample(seed=keys[0], sample_shape=(n_samples,)),
prior_dists['x0'].sample(seed=keys[1], sample_shape=(n_samples,)),
prior_dists['x1'].sample(seed=keys[2], sample_shape=(n_samples,)),
prior_dists['c'].sample(seed=keys[3], sample_shape=(n_samples,))
])
else:
if fit_sigma:
keys = jax.random.split(rng_key, 6)
return jnp.column_stack([
prior_dists['z'].sample(seed=keys[0], sample_shape=(n_samples,)),
prior_dists['t0'].sample(seed=keys[1], sample_shape=(n_samples,)),
prior_dists['x0'].sample(seed=keys[2], sample_shape=(n_samples,)),
prior_dists['x1'].sample(seed=keys[3], sample_shape=(n_samples,)),
prior_dists['c'].sample(seed=keys[4], sample_shape=(n_samples,)),
prior_dists['log_sigma'].sample(seed=keys[5], sample_shape=(n_samples,))
])
else:
keys = jax.random.split(rng_key, 5)
return jnp.column_stack([
prior_dists['z'].sample(seed=keys[0], sample_shape=(n_samples,)),
prior_dists['t0'].sample(seed=keys[1], sample_shape=(n_samples,)),
prior_dists['x0'].sample(seed=keys[2], sample_shape=(n_samples,)),
prior_dists['x1'].sample(seed=keys[3], sample_shape=(n_samples,)),
prior_dists['c'].sample(seed=keys[4], sample_shape=(n_samples,))
])
if fix_z:
n_params_total = 4
else:
n_params_total = 5
if fit_sigma:
n_params_total += 1
Initialise the nested sampling algorithm#
num_mcmc_steps = n_params_total * NS_SETTINGS['num_mcmc_steps_multiplier']
# Initialise the nested sampling algorithm using Blackjax
print("Setting up nested sampling algorithm...")
algo = blackjax.ns.adaptive.nss(
logprior_fn=logprior,
loglikelihood_fn=compute_single_loglikelihood,
n_delete=NS_SETTINGS['n_delete'],
num_mcmc_steps=num_mcmc_steps
)
# Initialise random key and generate initial particles
rng_key = jax.random.PRNGKey(0)
rng_key, init_key = jax.random.split(rng_key)
initial_particles = sample_from_priors(init_key, NS_SETTINGS['n_live'])
print("Initial particles generated, shape:", initial_particles.shape)
# Initialise the sampler state
state = algo.init(initial_particles, compute_single_loglikelihood)
# Define a one-step function for the nested sampling (JIT compiled for efficiency)
@jax.jit
def one_step(carry, xs):
state, k = carry
k, subk = jax.random.split(k, 2)
state, dead_point = algo.step(subk, state)
return (state, k), dead_point
Setting up nested sampling algorithm...
Initial particles generated, shape: (200, 4)
Running the Nested Sampling#
Now we run the nested sampling algorithm for a specified number of iterations. The loop stops if the evidence of the live points is sufficiently lower than that of the dead points. Progress is printed every 10 iterations.
dead = []
# num_iterations = NS_SETTINGS['max_iterations']
print("Running nested sampling...")
with tqdm.tqdm(desc="Dead points", unit=" dead points") as pbar:
while (not state.sampler_state.logZ_live - state.sampler_state.logZ < -3):
(state, rng_key), dead_info = one_step((state, rng_key), None)
dead.append(dead_info)
pbar.update(NS_SETTINGS['n_delete'])
# if i % 10 == 0:
# print(f"Iteration {i}: logZ = {state.sampler_state.logZ:.2f}")
# Combine dead points and compute log evidence
dead = jax.tree_map(lambda *args: jnp.concatenate(args), *dead)
logw = log_weights(rng_key, dead)
logZs = jax.scipy.special.logsumexp(logw, axis=0)
print(f"Runtime evidence: {state.sampler_state.logZ:.2f}")
print(f"Estimated evidence: {logZs.mean():.2f} ± {logZs.std():.2f}")
Running nested sampling...
Dead points: 3020 dead points [03:52, 13.01 dead points/s]
Runtime evidence: -160.40
Estimated evidence: -161.47 ± 0.29
Post-Processing and Plotting#
After running the nested sampling procedure, we process the samples by saving the chains and creating a corner plot to visualise the posterior distributions. The anesthetic package is used for the 2D plots.
# Define parameter names based on whether redshift is fixed or sigma is fit
if fix_z:
param_names = ['t0', 'log_x0', 'x1', 'c']
else:
param_names = ['z', 't0', 'log_x0', 'x1', 'c']
if fit_sigma:
param_names.append('log_sigma')
# Save the chains of dead points
save_chains_dead_birth(dead, param_names)
# Read the chains using anesthetic
samples = read_chains('chains/chains', columns=param_names)
# Create a corner plot of the posterior distributions
fig, axes = make_2d_axes(param_names, figsize=(10, 10), facecolor='w')
samples.plot_2d(axes, alpha=0.9, label="posterior")
axes.iloc[-1, 0].legend(bbox_to_anchor=(len(axes)/2, len(axes)), loc='lower center', ncols=2)
plt.savefig('corner_plot.png')
plt.show()
print("Corner plot saved as 'corner_plot.png'.")
Saved 3020 samples to chains/chains_dead-birth.txt
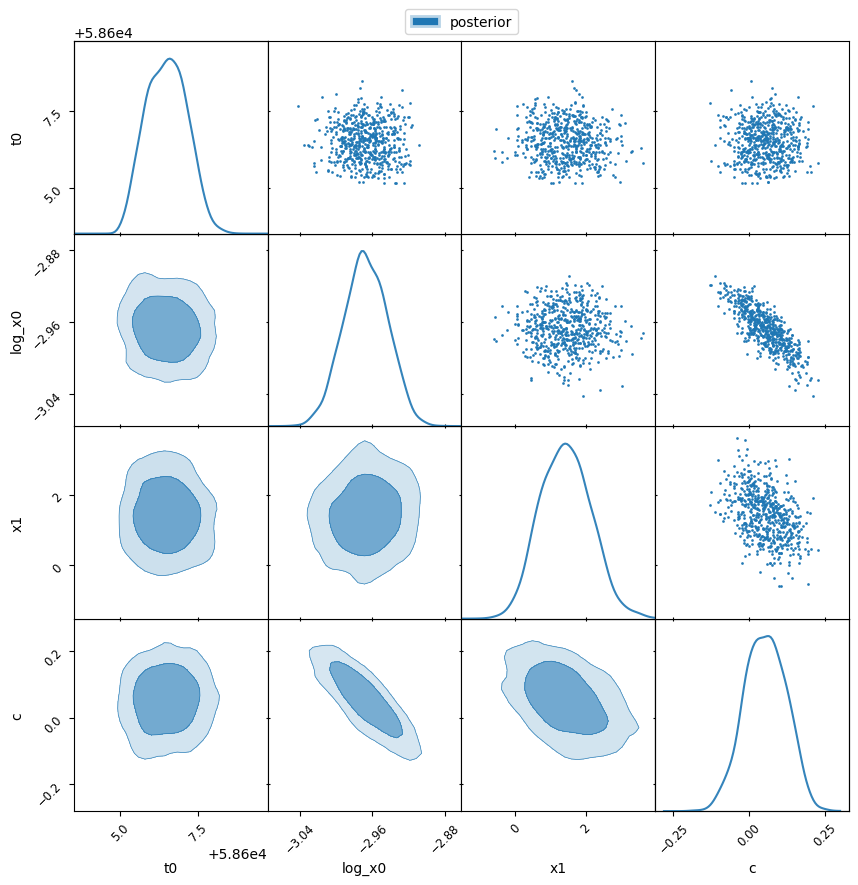
Corner plot saved as 'corner_plot.png'.
Parameter Statistics#
Finally, we print a summary of the fitted parameters, showing the mean and standard deviation for each parameter based on the posterior samples.
print("\nParameter Statistics:")
print("-" * 50)
for param in param_names:
mean = samples[param].mean()
std = samples[param].std()
print(f"{param}: {mean:.6f} ± {std:.6f}")
Parameter Statistics:
--------------------------------------------------
t0: 58606.500621 ± 0.636398
log_x0: -2.967442 ± 0.023847
x1: 1.440318 ± 0.704653
c: 0.052617 ± 0.067823
