Custom Inner MCMC Kernels#
The common top level API presented in other notebooks, nss is unfamiliar to those used to the SMC implementations in blackjax. It is a fusion of the generic outer NS kernel with a particular inner kernel, slice sampling.
It is instructive then to examine both how this combination is built, and how one could combine a new choice of inner MCMC kernel with the slice sampling procedure.
import tqdm
import jax
import jax.numpy as jnp
from functools import partial
from blackjax.ns.adaptive import build_kernel, init
from blackjax.ns.base import new_state_and_info, delete_fn
from blackjax.ns.utils import repeat_kernel, finalise
from blackjax.mcmc.random_walk import build_rmh, RWState
from blackjax import SamplingAlgorithm
Setting up a constrained random walk#
To be compatible with nested sampling we have to address two oddities with respect to other algorithms in blackjax:
We need to implement a constrained random walk, rather than purely accepting based on a metropolis acceptance ratio, there is an additional imposed constraint.
To perform the post run reconstruction we need to record the value of the constraint (likelihood), rather than just operating on a density
To do this let’s construct a random walk kernel in the usual blackjax style, and address these two issues
(We also include the kernel tuning for a basic random walk here)
mcmc_kernel = build_rmh()
def random_walk_kernel(rng_key, state, logprior_fn, loglikelihood_fn, loglikelihood_0, params):
def proposal_distribution(rng_key, position):
"""
Proposes a new position by adding Gaussian noise to the current position.
The noise is scaled by the 'sigma' parameter that our tuning function will set.
"""
step = params['sigma'] * jax.random.normal(rng_key, shape=position.shape)
return position + step
mcmc_state = RWState(position=state.position, logdensity=state.logprior)
new_mcmc_state, mcmc_info = mcmc_kernel(rng_key, mcmc_state, logprior_fn, proposal_distribution)
# As the walk occurs in the prior, we need to separately compute the loglikelihood
loglikelihood = loglikelihood_fn(new_mcmc_state.position)
# Now use a ns.utils function to construct a PartitionedState, a wrapper of the above MCMC state to include the likelihood
new_state, info = new_state_and_info(
position=new_mcmc_state.position,
logprior=new_mcmc_state.logdensity,
loglikelihood=loglikelihood,
info=mcmc_info,
)
# Accept if the loglikelihood is greater than the threshold
new_state = jax.lax.cond(
loglikelihood > loglikelihood_0,
lambda _: new_state,
lambda _: state,
operand=None,
)
return new_state, info
def update_random_walk_kernel_params(state, info, params):
"""A basic tuning function that updates the std of the particles."""
sigma = state.particles.std(axis=0)
return {'sigma': sigma}
Using the adaptive NS functions#
We now need to compose this set inner kernel with the Nested Sampling “outer” kernel
Note: We do not check that an MCMC step has been successful here, so may incur some spurious autocorrelation
def ns_mcmc(
logprior_fn,
loglikelihood_fn,
num_delete=10,
num_inner_steps=10,
):
"""
Build a nested sampling MCMC algorithm. This emulates how the `nss` top level api works,
Parameters
----------
logprior_fn : callable
Function that computes the log prior probability of the parameters.
loglikelihood_fn : callable
Function that computes the log likelihood of the parameters.
num_delete : int
Number of particles to delete at each step.
num_inner_steps : int
Number of inner MCMC steps to perform.
Returns
-------
init_fn : callable
Function to initialize the nested sampling state.
step_fn : callable
Function to perform a single step of nested sampling.
"""
inner_kernel = repeat_kernel(num_repeats=num_inner_steps)(random_walk_kernel)
_delete_fn = partial(delete_fn, num_delete=num_delete)
step_fn = build_kernel(
logprior_fn,
loglikelihood_fn,
_delete_fn,
inner_kernel,
update_random_walk_kernel_params,
)
init_fn = partial(
init,
logprior_fn=logprior_fn,
loglikelihood_fn=loglikelihood_fn,
update_inner_kernel_params_fn=update_random_walk_kernel_params,
)
return SamplingAlgorithm(init_fn, step_fn)
Problem definition#
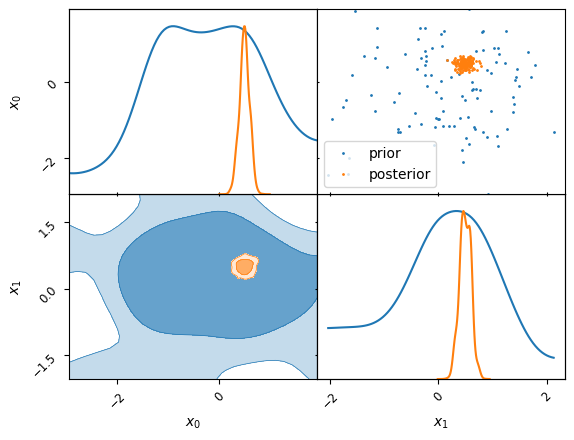
Define a small fitting problem of a 2D Gaussian
μ = 0.5
σ = 0.1
μ0 = 0.0
σ0 = 1.0
loglikelihood_fn = lambda x: jax.scipy.stats.norm.logpdf(x, loc=μ, scale=σ).sum()
logprior_fn = lambda x: jax.scipy.stats.norm.logpdf(x, loc=μ0, scale=σ0).sum()
rng_key = jax.random.PRNGKey(0)
num_live = 100
num_delete = 50
num_dims = 2
rng_key, prior_key = jax.random.split(rng_key)
particles = jax.random.normal(prior_key, (num_live, num_dims)) * σ0 + μ0
This can be run in a similar way and exported to the plotting tools. Note this inner kernel is not expected to perform well in high dimension or for more complex processes so should be considered more of a pedagogical example
nested_sampler = ns_mcmc(
logprior_fn=logprior_fn,
loglikelihood_fn=loglikelihood_fn,
num_delete=num_delete,
num_inner_steps=10,
)
init_fn = jax.jit(nested_sampler.init)
step_fn = jax.jit(nested_sampler.step)
live = init_fn(particles)
dead = []
with tqdm.tqdm(desc="Dead points", unit=" dead points") as pbar:
while not live.logZ_live - live.logZ < -3:
rng_key, subkey = jax.random.split(rng_key, 2)
live, dead_info = step_fn(subkey, live)
dead.append(dead_info)
pbar.update(num_delete)
dead = finalise(live, dead)
Dead points: 600 dead points [00:00, 830.76 dead points/s]
from anesthetic import NestedSamples
columns = [f"x{i}" for i in range(num_dims)]
labels = [f"$x_{i}$" for i in range(num_dims)]
samples = NestedSamples(
dead.particles,
logL=dead.loglikelihood,
logL_birth=dead.loglikelihood_birth,
columns=columns,
labels=labels,
logzero=jnp.nan,
dtype=jnp.float64,
)
a=samples.set_beta(0.0).plot_2d(columns, label="prior")
samples.set_beta(1.0).plot_2d(a, label="posterior")
a.iloc[0, 1].legend()
<matplotlib.legend.Legend at 0x308aa4550>